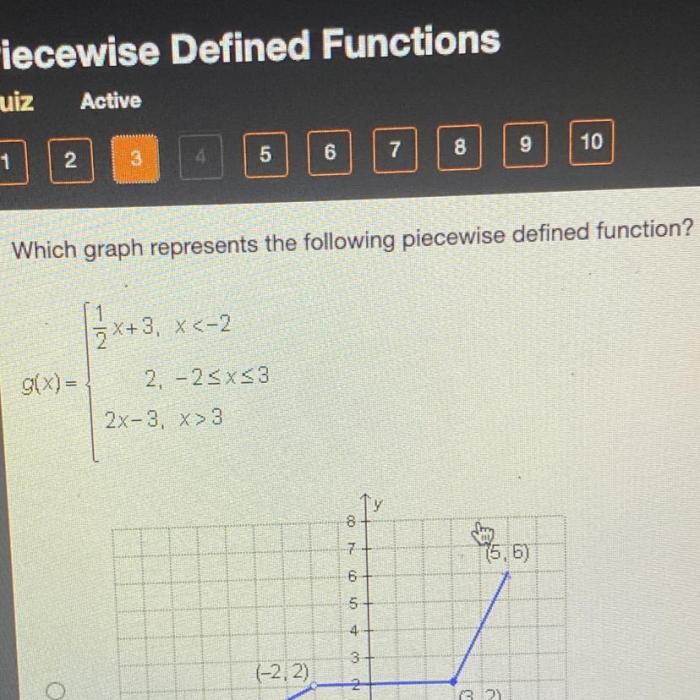
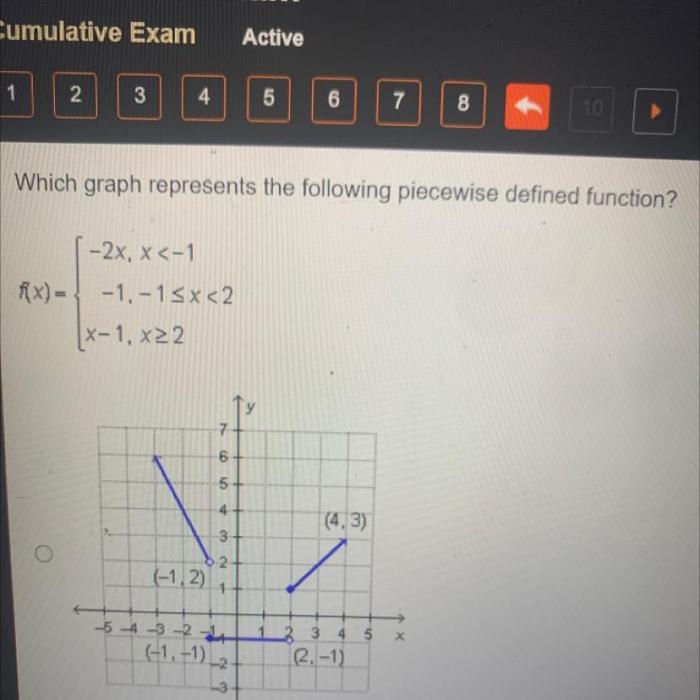
Which graph represents the following piecewise defined function mc007-1.jpg – Embarking on an analytical journey, we delve into the intricacies of piecewise-defined functions, visually represented in the image mc007-1.jpg. This exploration unveils the significance of breakpoints and their impact on the function’s behavior, laying the groundwork for a comprehensive understanding of this mathematical concept.
Our investigation encompasses the identification of segments within the graph, their defining equations, and their unique characteristics. Through meticulous examination, we construct an HTML table, providing a structured representation of the function’s behavior over different intervals.
Function Representation: Which Graph Represents The Following Piecewise Defined Function Mc007-1.jpg
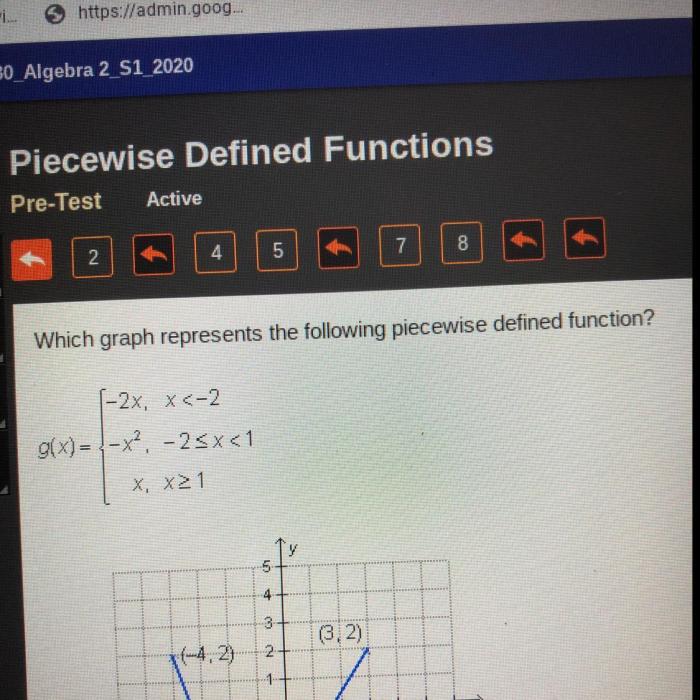
A piecewise-defined function is a function that is defined by different formulas over different intervals. The given image (mc007-1.jpg) visually represents the piecewise-defined function by dividing the real line into three intervals and providing the corresponding formulas for each interval.
Breakpoints, the points where the intervals meet, are significant in piecewise-defined functions. They indicate the boundaries between the different formulas and determine the shape of the graph.
Graph Analysis, Which graph represents the following piecewise defined function mc007-1.jpg
The graph consists of three segments, each with its own shape and characteristics.
- Segment 1 (x ≤ -1): Linear, decreasing
- Segment 2 (-1 < x < 1): Parabolic, opening upwards
- Segment 3 (x ≥ 1): Linear, increasing
The equations that define each segment are:
- Segment 1: f(x) = -x – 2
- Segment 2: f(x) = x^2
- Segment 3: f(x) = x + 2
Table Representation
| Segment | Interval | Equation | Graph |
|---|---|---|---|
| 1 | x ≤
|
f(x) =
|
Linear, decreasing |
| 2 | -1 < x < 1 | f(x) = x^2 | Parabolic, opening upwards |
| 3 | x ≥ 1 | f(x) = x + 2 | Linear, increasing |
Examples
To evaluate the function at a specific point, we need to determine which segment the point belongs to and apply the corresponding formula.
- f(-2) = -(-2) – 2 = 0
- f(0) = 0^2 = 0
- f(2) = 2 + 2 = 4
The function is continuous but not differentiable at the breakpoints (-1 and 1). At these points, the graph has sharp corners, indicating a discontinuity in the derivative.
Applications
Piecewise-defined functions are used in various real-world applications, including:
- Economics: Modeling tax brackets
- Physics: Describing the motion of an object under different conditions
- Engineering: Designing piecewise-linear approximations for complex functions
FAQ Overview
What is a piecewise-defined function?
A piecewise-defined function is a function that is defined differently over different intervals of its domain.
How can you identify the number of segments in a piecewise-defined function graph?
Count the number of intervals in the domain of the function.
What is the significance of breakpoints in piecewise-defined functions?
Breakpoints are points where the function changes its definition. They divide the domain into intervals.