Quiz 1 area of polygons – Quiz 1: Area of Polygons embarks on an enthralling journey into the fascinating realm of geometry, where we delve into the intricacies of polygons and their enigmatic areas. From triangles to trapezoids, this exploration unravels the secrets of these geometric wonders, providing a comprehensive understanding of their measurement and significance in our world.
As we traverse this mathematical landscape, we will encounter formulas that empower us to calculate polygon areas with precision. We will dissect irregular polygons, employing clever techniques to determine their elusive areas. And we will uncover the practical applications of polygon area calculations, ranging from architecture to land surveying.
Define the Area of Polygons
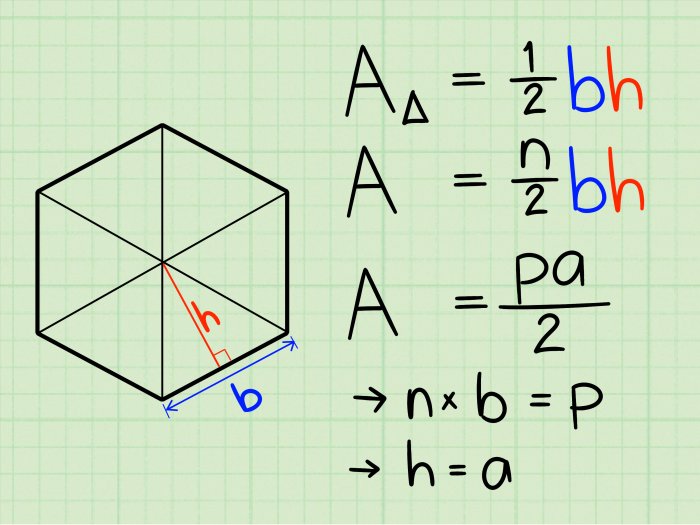
In geometry, the area of a polygon refers to the amount of two-dimensional space that the polygon occupies on a flat surface. It measures the extent or size of the polygon’s interior region.
Mathematically, the area of a polygon can be defined as the measure of the region enclosed by its sides. It is expressed in square units, such as square centimeters (cm 2), square meters (m 2), or square kilometers (km 2).
Units of Area, Quiz 1 area of polygons
The choice of area units depends on the size and context of the polygon being measured. For small polygons, square centimeters or square inches are commonly used. For larger polygons, such as land areas or building floor plans, square meters or square feet are more appropriate.
Quiz 1 on the area of polygons was a breeze! For those who need a refresher, check out this helpful resource . The formulas and examples will get you back on track in no time. Once you’ve brushed up on the basics, you’ll be ready to ace the next quiz on the area of polygons.
In scientific and engineering applications, square kilometers or square miles may be used to measure vast areas.
Formulas for Calculating the Area of Polygons
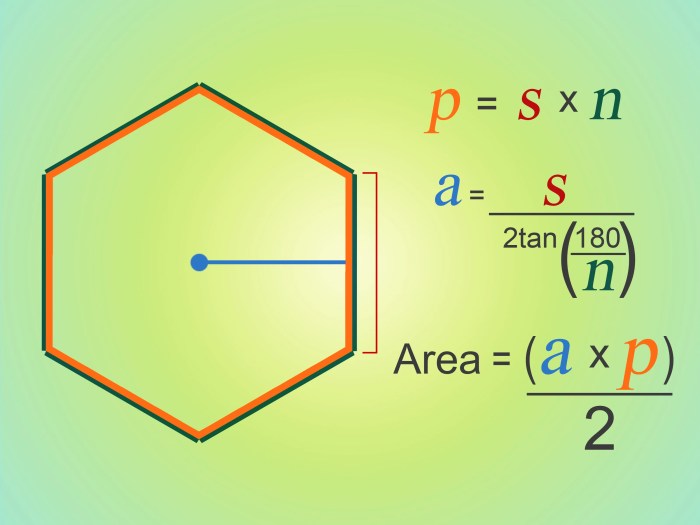
In geometry, the area of a polygon is the measure of the two-dimensional space enclosed by its sides. Different types of polygons have different formulas for calculating their areas.
Triangle
The area of a triangle can be calculated using the formula:
A = (1/2)
- b
- h
where:
- A is the area of the triangle
- b is the length of the base of the triangle
- h is the height of the triangle
Parallelogram
The area of a parallelogram can be calculated using the formula:
A = b
h
where:
- A is the area of the parallelogram
- b is the length of the base of the parallelogram
- h is the height of the parallelogram
Trapezoid
The area of a trapezoid can be calculated using the formula:
A = (1/2)
- (b1 + b2)
- h
where:
- A is the area of the trapezoid
- b1 is the length of the first base of the trapezoid
- b2 is the length of the second base of the trapezoid
- h is the height of the trapezoid
Regular Polygon
The area of a regular polygon can be calculated using the formula:
A = (1/2)
- P
- a
where:
- A is the area of the regular polygon
- P is the perimeter of the regular polygon
- a is the apothem of the regular polygon
Methods for Finding the Area of Irregular Polygons: Quiz 1 Area Of Polygons
Determining the area of irregular polygons requires different approaches compared to regular polygons. Here are three widely used methods:
Decomposition Method
This method involves breaking down the irregular polygon into smaller, simpler shapes, such as triangles, rectangles, or trapezoids. Once the areas of these individual shapes are calculated, they can be added together to obtain the total area of the irregular polygon.
Triangulation Method
In this method, the irregular polygon is divided into a series of triangles by drawing diagonals from one vertex to another. The area of each triangle can then be calculated using the formula for the area of a triangle (A = 1/2 – base – height).
The sum of the areas of all the triangles gives the total area of the irregular polygon.
Geometric Shapes Approximation
This method involves approximating the area of the irregular polygon by superimposing a geometric shape, such as a circle or an ellipse, over the polygon. The area of the geometric shape can then be calculated and used as an approximation of the area of the irregular polygon.
Applications of Polygon Area Calculations
Polygon area calculations find practical applications in various fields, including architecture, land surveying, and everyday life.
Calculating the Area of a Complex Room
To calculate the area of a room with an irregular shape, divide it into simpler polygons (e.g., rectangles, triangles). Calculate the area of each polygon and sum them to get the total area.
Polygon Area Calculations in Land Surveying
Land surveyors use polygon area calculations to determine the size and boundaries of land parcels. This information is crucial for land ownership, property taxes, and land use planning.
Polygon Area Calculations in Architecture and Design
Architects and designers use polygon area calculations to optimize space utilization and plan building layouts. They calculate the area of rooms, floor plans, and other architectural elements to ensure efficient use of space.
Essential Questionnaire
What is the formula for calculating the area of a triangle?
Area = (1/2) – base – height
How do I find the area of an irregular polygon?
You can use the decomposition method or the triangulation method to approximate the area of an irregular polygon.
What are some real-world applications of polygon area calculations?
Polygon area calculations are used in architecture, land surveying, and design to determine the area of rooms, land parcels, and other geometric shapes.